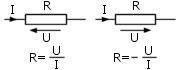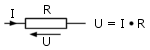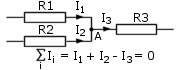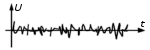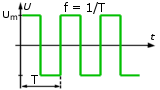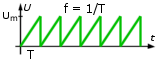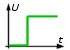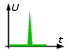Podstawowe prawa

Dwie najważniejsze wielkości, których zachowanie w układach elektronicznych poddawane jest obserwacji i analizie to napięcie U oraz prąd I.
Napięcie między dwoma punktami jest to wydatek energii (wykonana praca), konieczny do przeniesienia jednostkowego ładunku dodatniego z punktu o niższym potencjale (bardziej ujemnym) do punktu o wyższym potencjale (bardziej dodatnim). Jednostką miary napięcia jest 1V (wolt). Można więc powiedzieć, że aby ładunek jednego kulomba pokonał różnicę potencjałów jednego wolta, należy wykonać pracę jednego dżula.
      Napięcie oznaczane jest zwykle symbolem U. Napięcie między punktami A i B jest oznaczane jako U_AB. Już dawno uzgodniono, że napięcie U_AB jest dodatnie, gdy punkt A jest dodatni względem punktu B, a U_AB jest ujemne, gdy punkt A jest ujemny względem punktu B. Obowiązuje również następująca zależność U_AB = -U_BA.

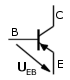
		Dla przykładu (rys. 1.1) zapis napięcia pomiędzy bazą, a emiterem tranzystora typu PNP (o tym w dziale tranzystory): UBE = -0,7V  lub  -UBE = 0,7V  lub  UEB = 0,7V oznacza, że między punktem E i B występuje napięcie 0,7V, a punkt E ma wyższy potencjał (jest bardziej dodatni) niż punkt B.       Często używa się określenia "napięcie w danym punkcie układu", należy to rozumieć jako napięcie między danym punktem, a punktem wspólnym (zerowym) najczęściej nazywanym "masą".
rys. 1.1
		Prąd wyraża szybkość przepływu ładunku elektrycznego obok pewnego punktu. Jednostką miary jest 1A (amper). Można więc powiedzieć, że prąd jednego ampera jest równy przepływowi ładunku jednego kulomba na sekundę.       Prąd oznaczany jest zwykle symbolem I, a kierunek jego przepływu zaznacza się strzałką na przewodzie. Uzgodniono, że prąd jest dodatni gdy strzałka jest skierowana od punktu bardziej dodatniego do punktu bardziej ujemnego, mimo że faktyczny kierunek przepływu elektronów jest przeciwny.       Tak naprawdę jest obojętne jak narysuje się strzałki prądu i napięcia w obwodzie (rys. 1.2), ważne jest, aby przyporządkować ich wartościom liczbowym właściwe znaki. Jeżeli strzałki prądu i napięcia, np. na rezystorze R są narysowane z przeciwnym zwrotem to R=U/I, a jeżeli zwroty są takie same to R=-U/I. Znak minus w ostatnim wzorze nie oznacza, że rezystancja jest ujemna, tylko informuje o takich samych zwrotach strzałek napięcia i prądu.
rys. 1.2
		Prawo Ohma mówi, że napięcie U na końcach przewodnika, przez który płynie prąd o natężeniu I jest iloczynem natężenia prądu i rezystancji R tego przewodnika, czyli U = I * R (rys. 1.3).       Jest to prawo, z którego będziesz wielokrotnie korzystał, gdy będziesz musiał obliczyć prąd lub napięcie czy też wyliczyć właściwą dla danego układu wartość rezystora.
rys. 1.3
		Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z niego lub inaczej, że suma wszystkich prądów w węźle jest równa zeru (rys. 1.4).       Prądy wpływające do węzła mają znak dodatni, a wypływające znak ujemny.       Przykładem węzła jest punkt A na rysunku. Prądy I1, I2 są dodatnie, a I3 ujemny.
rys. 1.4
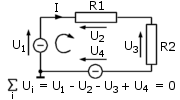
		Drugie prawo Kirchhoffa mówi, że w obwodzie zamkniętym (oczku) suma wszystkich napięć jest równa zeru (rys. 1.5).       Napięcia, których zwrot strzałki jest zgodny z obiegiem oczka są dodatnie, a te, których zwrot jest przeciwny są ujemne. Obieg oczka przyjmuje się zgodnie z zaznaczoną okrągłą strzałką wewnątrz obwodu.       Zgodnie z tymi założeniami napięcia U1 i U4 są dodatnie, a U2 i U3 ujemne.
rys. 1.5
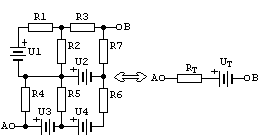
		Twierdzenie Thevenina mówi, że dowolny dwuzaciskowy układ, składający się z kombinacji źródeł napięcia i rezystorów można zastąpić szeregowo połączonymi ze sobą pojedynczego rezystora i pojedynczego źródła napięciowego.    Inaczej mówiąc mieszaninę rezystorów i baterii można zastąpić jednym rezystorem i jedną baterią tak jak pokazane to jest na rys. 1.6.    Wypadkowe theveninowskie rezystancja i napięcie wynoszą wówczas RT i UT. Ich wartości można wyznaczyć w sposób bardzo prosty. Napięcie UT jest napięciem na rozwartych zaciskach theveninowskiego układu zastępczego, a więc jeśli oba układy mają się zachowywać tak samo to musi to być również napięcie na rozwartych zaciskach układu pierwotnego. Napięcie to można wyliczyć lub zmierzyć. Rezystancję RT można znaleźć wiedząc, że prąd zwarcia układu zastępczego jest równy UT/RT lub inaczej mówiąc UT=U(rozwarcia) RT=U(rozwarcia)/I(zwarcia)    Z twierdzenia Thevenina korzysta się bardzo często , a szczególnie tam gdzie mamy do czynienia z łączeniem układów wzajemnie się obciążających, gdzie trzeba określić wielkość rezystancji obciążającej tak aby nie wpływała ona w znaczącym stopniu na obciążany układ. Najprostszym przykładem jest obciążanie dzielnika napięcia gdzie do określenia wzajemnych zależności między obciążeniem a wartościami rezystorów dzielnika wykorzystuje się twierdzenie Thevenina.
rys. 1.6
		Moc (inaczej mówiąc praca wykonana w jednostce czasu) pobierana przez dowolne urządzenie (np. rezystor) jest równa:  P = U * I       Dla napięcia U w woltach (V) i prądu I w amperach (A) otrzymuje się moc P w watach (W).       Korzystając z prawa Ohma (rys. 1.3) można otrzymać zależności, które przydadzą się np. przy określaniu mocy rezystorów: P = I^2 * R oraz P = U^2/R.       Moc najczęściej zamienia się w ciepło, aby się o tym przekonać wystarczy dotknąć obudowy dowolnego urządzenia elektronicznego podczas jego pracy. Abyś mógł w pełni zrozumieć układy elektroniczne, w których mamy do czynienia ze zmieniającymi się w czasie napięciem, musisz poznać najbardziej typowe rodzaje sygnałów (tak właśnie nazywa się napięcia zmieniające się w czasie w określony sposób).

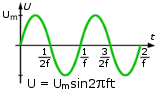
		Sygnał sinusoidalny jest przedstawiony na rys. 1.7. Wzór opisujący ten sygnał wygląda następująco: U = Umsin2pft, gdzie: Um - amplituda, f - częstotliwość wyrażona w hercach (Hz), t - czas w sekundach.       Jeśli przyjąć, że w=2pf, to sygnał sinusoidalny można opisać następującym wzorem: U = Umsinwt, gdzie w jest pulsacją wyrażoną w radianach na sekundę.       Falę sinusoidalną opisują dwa parametry amplituda i częstotliwość (dotyczy to również innych sygnałów). Czasami zamiast amplitudy używa się pojęcia wartości skutecznej Usk czy też wartości międzyszczytowej Upp.       Wartość skuteczna jest równa Usk=0,707*Um, natomiast wartość międzyszczytowa jest równa podwojonej amplitudzie Upp=2Um.       Przykładem wartości skutecznej sygnału sinusoidalnego może być znana wszystkim wartość 220V napięcia o częstotliwości 50Hz w gnieździe sieciowym, jakie znajduje się w każdym mieszkaniu. Amplituda tego napięcia wynosi 311V, a wartość międzyszczytowa 622V.
rys. 1.7
		Szum przedstawiony na rys. 1.8 jest nieodłącznym towarzyszem sygnałów użytecznych i jest czymś niepożądanym w układach elektronicznych, a w szczególności w układach pomiarowych o dużej czułości. Najczęstszym rodzajem szumów jest szum pochodzenia termicznego wytwarzany przez rezystory.
rys. 1.8
		Sygnał prostokątny ma kształt pokazany na rys. 1.9 i podobnie jak sygnał sinusoidalny można go opisać dwoma parametrami, czyli amplitudą i częstotliwością, z tą różnicą, że wartość skuteczna dla fali prostokątnej jest równa jej amplitudzie. Często zamiast częstotliwości używa się pojęcia okres T, który jest równy T=1/f.       Sygnał prostokątny składa się ze zbocza narastającego, poziomu wysokiego, zbocza opadającego i poziomu niskiego. Nie zawsze sygnał prostokątny wygląda tak jak na rysunku. Najczęściej spotyka się sygnał prostokątny tylko z "dodatnimi połówkami" to znaczy, że poziom niski jest w granicach 0V. Kształt jego jest również daleki od ideału, gdyż zbocza nie są prostopadłe (rys. 1.10). Najczęściej czas narastania czy opadania zboczy mieści się w granicach od kilku nanosekund (ns) do kilku mikrosekund (ms) i mierzy się go jako czas narastania od 0,1 do 0,9 napięcia sygnału.       Z sygnałami prostokątnymi mamy do czynienia nie tylko w układach cyfrowych, ale również na styku elektroniki analogowej i cyfrowej w takich układach jak komparatory, przetworniki A/C czy C/A, multipleksery analogowe.
rys. 1.9
rys. 1.10
		Sygnał piłokształtny jest przedstawiony na rys. 1.11. Faktycznie przypomina on zęby piły. Jest to sygnał o przebiegu liniowym, czyli takim, w którym napięcie rośnie lub opada ze stałą prędkością do określonej wartości i powtarzany jest okresowo.
rys. 1.11
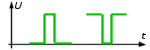
		Impulsy mogą przybierać kształty przedstawione na rys. 1.12. Najczęściej nie są to sygnały okresowe to znaczy nie powtarzają się w sposób regularny w czasie. Opisać je można poprzez podanie amplitudy i szerokości impulsu.       W technice cyfrowej mamy jednak do czynienia również z impulsami powtarzającymi się okresowo, wtedy do opisu takiego sygnału dodajemy częstotliwość lub okres, oraz możemy również mówić o współczynniku wypełnienia, czyli stosunku szerokości impulsu do okresu powtarzania. Impulsy dzielimy na dodatnie (pierwszy impuls od lewej na rys. 1.12) i ujemne (drugi impuls od lewej na rys. 1.12).
rys. 1.12

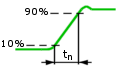
			Skoki i szpilki są w zasadzie sygnałami, które nie mają praktycznego zastosowania w układach elektronicznych, nadają się za to znakomicie do ich analizowania i opisu. Skok przedstawiony na rys. 1.13 jest częścią sygnału prostokątnego, natomiast szpilka pokazana na rys. 1.14 jest po prostu bardzo wąskim impulsem.
rys. 1.13	rys. 1.14

ku	kulog
0,1	-20dB
0,707	-3dB
1	0dB
1,41	3dB
10	20dB
100	40dB
1000	60dB
tab. 1.1

Decybel został wymyślony po to, aby ułatwić porównywanie amplitud dwóch sygnałów, szczególnie gdy różnica między nimi jest bardzo duża i wygodniej jest używać wtedy miary logarytmicznej.
      Stosunek amplitud dwóch sygnałów można wyrazić w decybelach zgodnie z poniższym wzorem:

k_ulog[dB]=20log₁₀(U₂/U₁)

gdzie U₂ i U₁ to amplitudy porównywanych sygnałów.
      Obok w tabeli 1.1 przedstawione są dla porównania liniowe i logarytmiczne stosunki amplitud sygnałów.

Przedrostek	Symbol	Wielokrotność
giga	G	10^9
mega	M	10^6
kilo	k	10^3
mili	m	10^-3
mikro	m	10^-6
nano	n	10^-9
piko	p	10^-12
tab. 1.2

Przedrostki. W elektronice posługujemy się jednostkami takimi jak wolt, ohm, amper, ale chyba jeszcze częściej ich tysięcznymi czy milionowymi częściami lub wielokrotnościami.
      Aby nie mówić czy pisać np.: jedna tysięczna ampera lub jeden milion herców posługujemy się przedrostkami i ich symbolami, i wtedy powiemy: jeden miliamper - 1mA, jeden megaherc - 1MHz.
      Należy zwrócić uwagę, że symbol jednostki zawsze piszemy bez odstępu po symbolu przedrostka. w tabeli 1.2 są przedstawione najczęściej używane przedrostki i ich symbole.